[Coding Test] 그래프 -1-

2024년 7월 15일 13 분 소요

그래프는 데이터를 표현하는 Node와 Node들을 연결하는 Edge로 구성된 집합을 의미한다.

트리 또한 그래프의 일종이다.

그래프의 표현

Edge List, 에지 리스트

배열을 이용하여 출발 노드와 도착 노드를 저장하여 에지를 중심으로 표현한다.

필요시에는 가중치를 저장하여 가중치가 있는 에지를 표현할 수 있다.

에지 리스트로 그래프 표현하기.

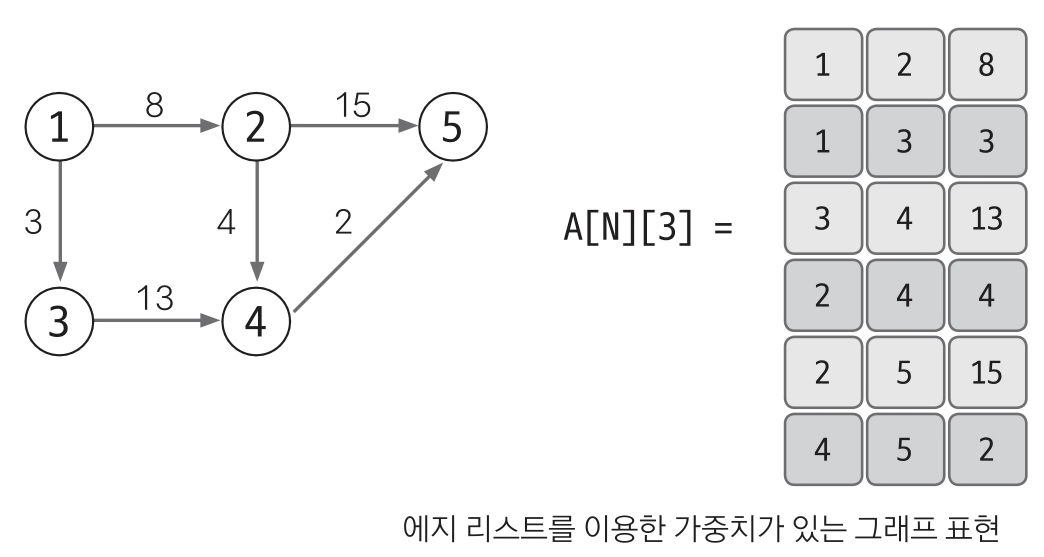
배열의 행은 가중치가 없다면 출발 노드와 도착 노드만으로 표현하기에 2개의 행을, 가중치를 표현한다면 3개의 행을 가진다.

에지 리스트로 그래프 표현하기 Do it! 알고리즘 코딩 테스트

1행은 시작 노드, 2행은 도착 노드이며 해당 예시에서는 한 방향으로만 표시했기에 1번 노드에서 2번 노드로 향하는 화살표를 그려준다.

여기서 3행에 해당하는 값이 가중치이다.

가중치가 필요 없다면 3행을 사용하지 않고 1,2 행만으로 그래프를 표현하면된다.

에지 리스트로 그래프를 표현하는 것은 어렵지 않지만 특정 노드와 관련되어 있는 에지를 탐색하기는 쉽지 않다.

흔히 벨만 포드, 크루스칼 알고리즘에 사용하며, 노드 중심 알고리즘에는 잘 사용하지 않는다.

Adjacency matrix, 인접 행렬

2차원 배열을 자료구조로 이용하여 그래프를 표현한다.

에지 리스트와 다르게 노드 중심의 그래프 표현 방법이다.

인접 행렬로 그래프 표현하기

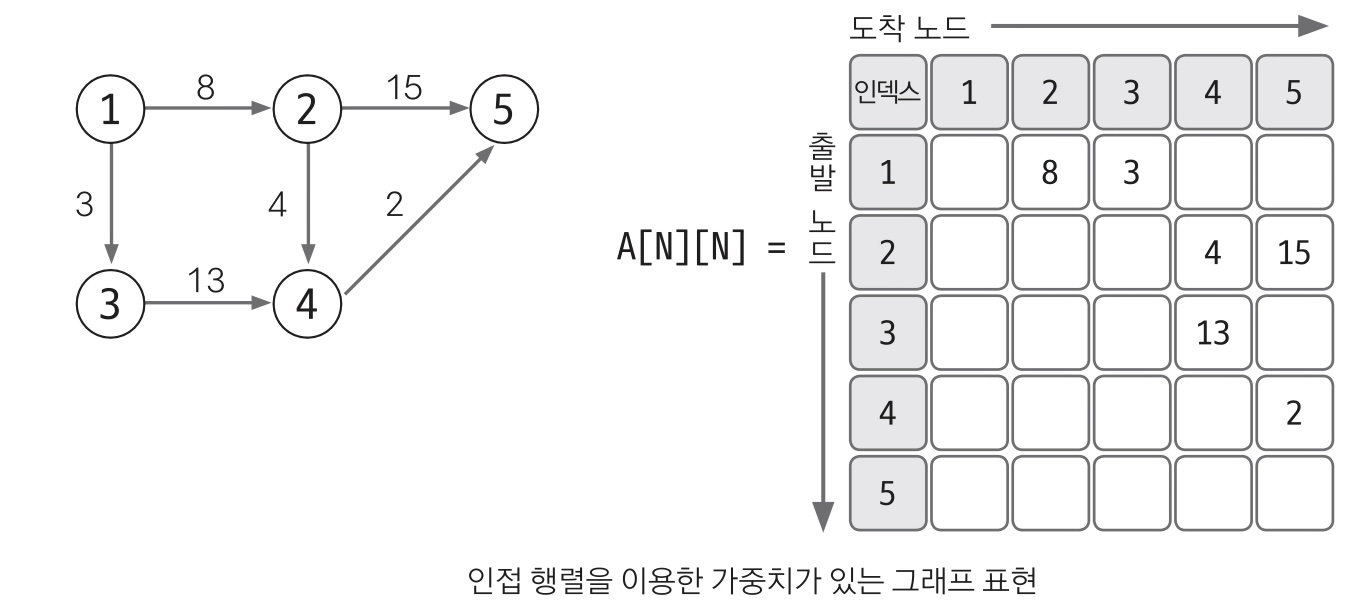
2차원 배열을 이용하여 x방향의 배열은 도착 노드로, y방향의 배열은 출발 노드로 설정한다.

레코드에 1이아닌 값이 들어가 있다면 이는 가중치를 표현하는 인접 행렬 그래프로 해석한다.

인접 행렬로 그래프 표현하기 Do it! 알고리즘 코딩 테스트

이 또한 에지 리스트와 같이 구현은 쉽다.

두 노드를 연결하는 에지의 여부와 가중치 값을 배열에 접근하면 바로 확인할 수 있는 것이 장점이다.

하지만 노드와 관련되어 있는 에지를 탐색하기 위해 N번 접근하기에 노드 개수에 비해 에지가 적다면 공간 효율성이 크게 떨어진다.

java에서 노드의 개수가 3만개가 넘는다면 java heap space 에러가 발생하는 것처럼 노드 개수가 많다면 2차원 배열 선언 자체가 불가능할 수 있기에 노드 개수에 따라 사용 여부를 적절하게 판단해야한다.

Adjacency list, 인접 리스트

노드의 개수만큼 ArrayList를 선언하여 그래프를 표현한다.

ArrayList Collections의 Generic 타입은 상황에 따라 변경하여 사용한다

인접 리스트로 그래프 표현하기

위에서 설명했듯이 노드의 개수만큼 ArrayList를 선언하여 해당 노드가 어떤 노드로 얼만큼의 가중치를 가질지를 선언해준다.

인접 리스트로 그래프 표현하기 Do it! 알고리즘 코딩 테스트

위의 예시에서는 1번 노드가 2번 노드로 8만큼의 가중치를 갖는 다는 것을 1 -> 2, 8 처럼 표현하였다.

즉, ArrayList[1] = [(2, 8), (3, 3)]와 같이 표현하며 (2,8) 은 Generic Type으로 선언하였던 사용자 객체인 Node로 표현된 것이다.

다른 방법들에 비해 구현은 복잡한 편이지만 노드와 연결되어 있는 에지를 탐색하는 시간은 매우 뛰어나며, 노드 개수가 커도 공간 효율이 좋기에 메모리 초과 에러도 발생하지 않는다.

이런 장점 때문에 코딩 테스트에선 인접 리스트를 이용한 그래프 구현을 선호한다.

아래의 문제를 풀어보면서 그래프를 익혀보자.

https://www.acmicpc.net/problem/18352

문제를 풀기 위해 그래프를 표현하면서 BFS의 탐색 과정을 거쳐야한다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {

    // 방문 표시를할 가중치 배열
    static int[] visited;
    // 그래프 정보
    static ArrayList<Integer>[] A;
    // input 값
    static int N,M,K,X;
    static List<Integer> answer;

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        // 도시(노드)의 개수
        N = Integer.parseInt(st.nextToken());

        // 도로(에지)의 개수
        M = Integer.parseInt(st.nextToken());

        // 거리(총 가중치)의 정보
        K = Integer.parseInt(st.nextToken());

        // 출발 도시(노드)의 정보
        X = Integer.parseInt(st.nextToken());

        // 노드의 개수 + 1 만큼 공간 초기화
        A = new ArrayList[N+1];

        answer = new ArrayList<>();

        // 노드의 개수만큼 ArrayList를 초기화한다.
        for(int i = 1; i <= N; i++){
            A[i] = new ArrayList<Integer>();
        }

        // 노드와 에지를 설정해준다.
        for(int i = 0; i < M; i++){
            st = new StringTokenizer(br.readLine());

            int start_node = Integer.parseInt(st.nextToken());
            int end_node = Integer.parseInt(st.nextToken());

            A[start_node].add(end_node);
        }

        // 방문 표시 배열 초기화
        visited = new int[N + 1];

        for(int i = 0; i <= N; i++){
            // 아직 방문하지 않았다는 의미에서 -1을 넣어준다.
            visited[i] = -1;
        }

        // 시작 위치부터 BFS 탐색을 수행
        bfs(X);

        // 이동 거리의 값이 문제에서 요구하는 거리와 같다면
        for (int i = 0; i <= N; i++){
            if (visited[i] == K){
                // 해당 노드를 출력하기 위해 저장한다.
                answer.add(i);
            }
        }

        //해당 되는 노드가 없다면 -1 출력
        if (answer.isEmpty()){
            System.out.println("-1");
        }
        // 해당되는 노드가 있다면 이를 출력한다.
        else {
            // 오름차순 출력을 위해
            Collections.sort(answer);
            for (int i : answer){
                System.out.println(i);
            }
        }

    }

    static void bfs(int node){
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.add(node);

        visited[node]++;

        while (!queue.isEmpty()){
            int current_node = queue.poll();

            for(int i : A[current_node]){
                // 방문하지 않은 요소는 -1로 초기화하였기에 방문하지 않은 노드가 있다면
                if (visited[i] == -1){
                    // 해당 노드의 값을 이전 노드의 방문 배열값 +1로 가중치를 더해준다.
                    // 이동 거리를 저장하는 의미.
                    visited[i] = visited[current_node] + 1;
                    queue.add(i);
                }
            }
        }
    }
}

Union-find, 유니온 파인드

여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 Union 연산과, 두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성되어있다.

핵심 이론

Union 연산

각 노드가 속한 집합을 1개로 합치는 연산이다. 노드 a가 A집합에 속하고, b가 B집합에 속한다면 union(a,b)은 A U B가 된다.

Find 연산

특정 노드 a에 관해 a가 속한 집합의 대표 노드를 반환하는 연산이다. 노드 a가 A집합에 속한다면 find(a)는 A 집합의 대표 노드를 반환한다.

유니온 파인드는 일반적으로 1차원 배열을 이용한다.

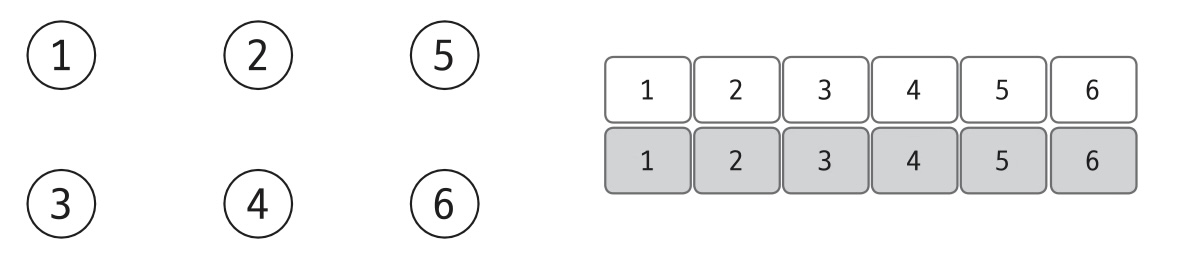
1. 처음에는 노드가 서로 연결되지 있지 않으므로 각 노드가 대표 노드가된다.

이에 따라 배열은 자신의 인덱스 값으로 초기화한다.

유니온 파인드 1 Do it! 알고리즘 코딩 테스트

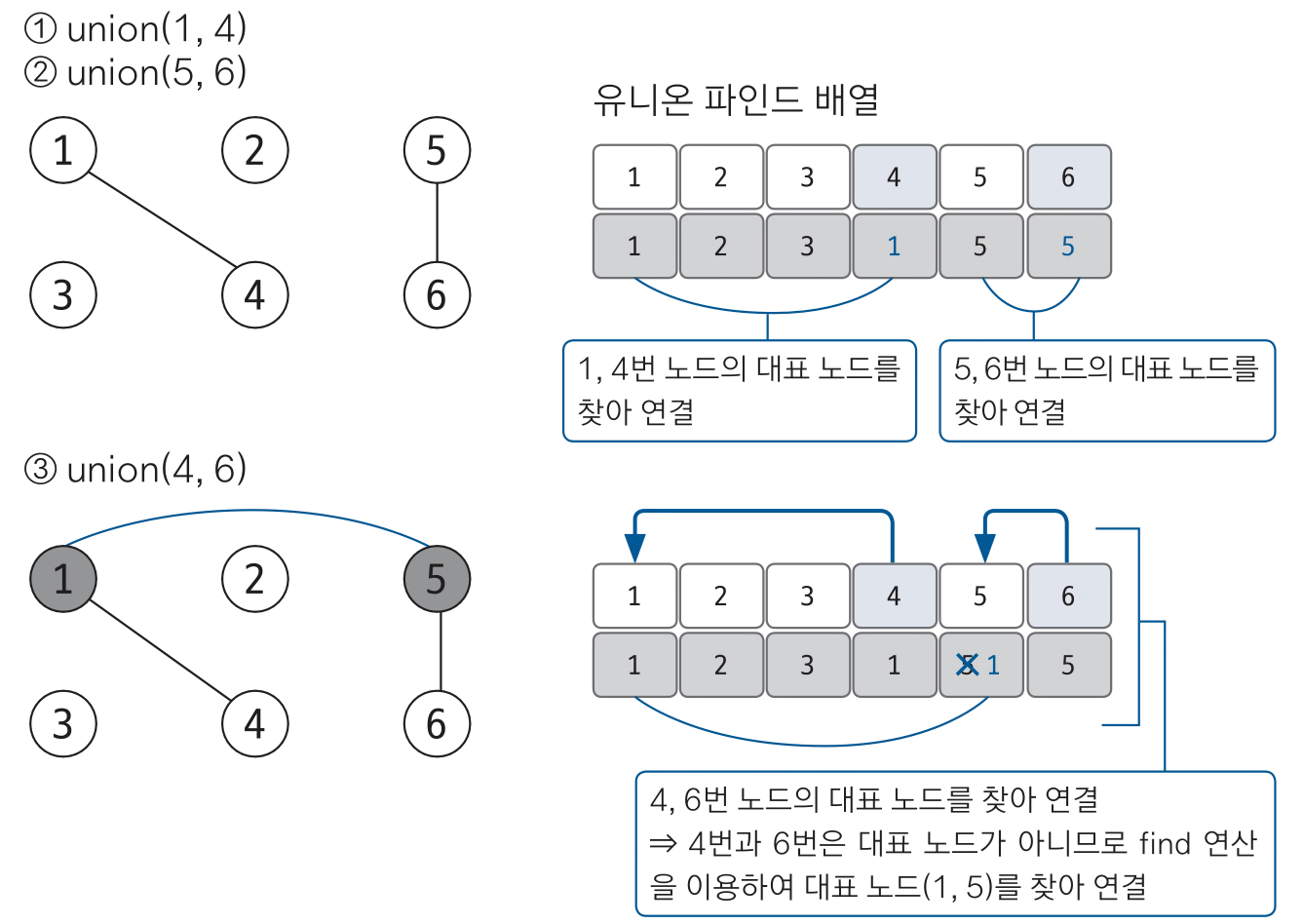
2. 2개의 노드를 선택하여 각각의 대표 노드를 찾아 연결하는 union 연산을 수행한다.

아래에서는 union(1,4), union(5,6)을 수행했다.

union(1,4)를 기준으로 설명하자면 1이 대표 노드가 되고 4는 자식 노드로 union 연산을 하므로 배열 [4]의 대표 노드를 1로 변경한다.

유니온 파인드 2 Do it! 알고리즘 코딩 테스트

이후 union(4,6)을 수행한다.

하지만 4와 6은 대표 노드가 아니기에 각 노드의 대표 노드를 찾아 올라간 후 대표 노드끼리 연결을 수행한다.

4의 대표 노드는 1, 6의 대표 노드는 5이므로 1,5 노드가 union되는데 4의 대표 노드가 1이므로 이를 부모노드로 6의 대표 노드인 5에 1을 대표 노드로 등록한다.

3. 자신이 속한 집합의 대표노드를 찾는 find 연산을 수행한다.

find 연산은 단순히 대표 노드를 찾는 역할뿐만 아닌 그래프를 정돈하고 시간 복잡도를 최적화 시킬 수 있다.

작동 원리는 아래와 같다.

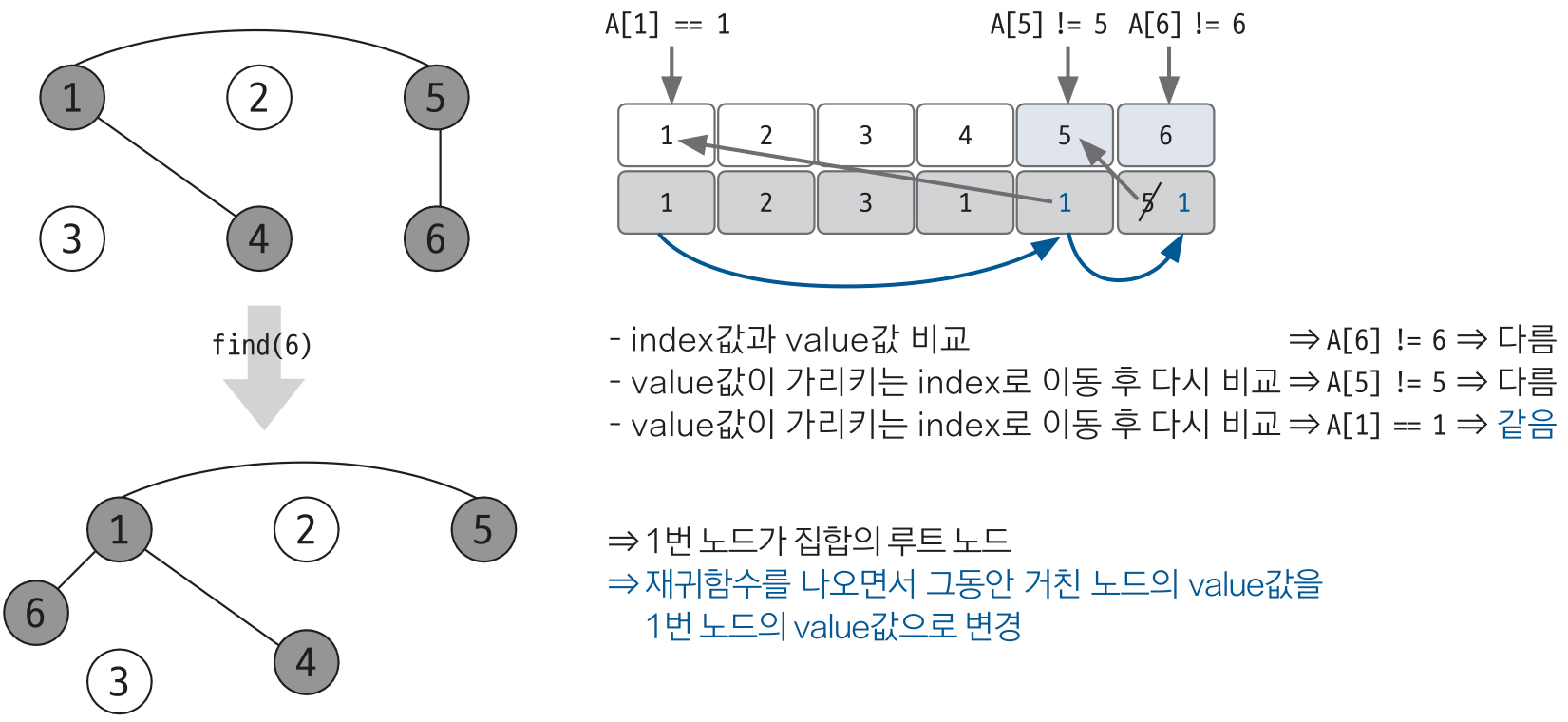
대상 노드 배열에 index 값과 value 값이 동일한지 확인한다.
동일하지 않으면 value에 해당하는 Node로 이동한다.
이동 위치의 index 값과 value 값이 같을 때 가지 1,2를 반복한다.(재귀 함수로 구현)
대표 노드에 도달했을 때 재귀 함수를 탈출하면서 거치는 모든 노드 값을 루트 노드 값으로 변경한다.

아래는 find(6)을 통해 루트 값을 찾는 동시에 자식 노드들의 값을 모두 부모 노드로 바꾸는 과정이다.

유니온 파인드 3 Do it! 알고리즘 코딩 테스트

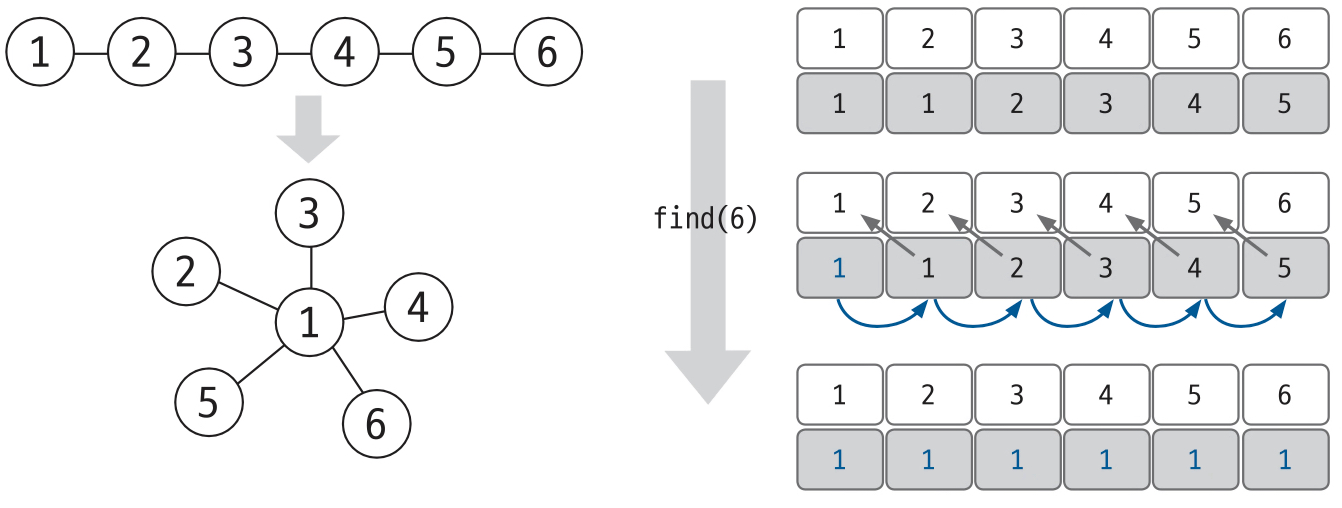
4. find 연산을 수행하여 시간 복잡도를 최적화한다.

최초 find 연산을 통해 통해 최적화를 마친 뒤 추후 노드와 관련된 find 연산은 O(1)의 시간 복잡도로 실행될 수 있다.

유니온 파인드 4 Do it! 알고리즘 코딩 테스트

아래의 문제를 풀면서 유니온 파인드를 익혀보자.

https://www.acmicpc.net/problem/1717

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {

    static int[] parent;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());

        // 원소 개수
        int N = Integer.parseInt(st.nextToken());

        // 수행할 질의 개수
        int M = Integer.parseInt(st.nextToken());

        // 노드의 관계를 나타낼 배열 초기화
        parent = new int[N+1];

        // 관계 형성 전 본인의 index 값으로 부모 노드를 초기화한다.
        for(int i = 1; i <= N; i++){
            parent[i] = i;
        }

        // 잘의 수행하기
        for(int i = 0; i < M; i++){
            st = new StringTokenizer(br.readLine());
            
            // 수행할 동작
            int action = Integer.parseInt(st.nextToken());
            
            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());

            // 첫 번째 숫자가 0이라면 union 수행
            if(action == 0){
                union(a, b);
            }
            // 0이 아닌, 1이라면 해당 요소들이 같은 집합의 원소인지 확인
            else {
                if(isSame(a, b)){
                    System.out.println("YES");
                }else{
                    System.out.println("NO");
                }
            }
        }
    }

    // 노드 끼리 union 연산
    private static void union(int a, int b){
        // 해당 노드의 부모 노드를 찾는다.
        a = find(a);
        b = find(b);

        // 서로 같지 않다면 union할 수 있다는 의미로 b노드에 a를 대표 노드로 등록한다.
        if(a != b){
            parent[b] = a;
        }
    }

    // 대표 노드 찾기 및 경로 압축
    private static int find(int a){
        // 노드의 대표 노드 값이 index와 같다면
        if(parent[a] == a){
            // 본인이 대표 노드이기 때문에 바로 return
            return a;
        }
        else {
            // 같지 않다면 재귀 함수로 찾려는 노드의 부모노드를 찾으며 경로를 압축을한다.
            return parent[a] = find(parent[a]);
        }
    }

    // 같은 집합의 원소인지 확인
    private static boolean isSame(int a, int b){
        a = find(a);
        b = find(b);

        if(a == b){
            return true;
        }
        return false;
    }
}

Topology Sort, 위상 정렬

사이클이 없는 방향 그래프에서 노드의 순서를 찾는 알고리즘이다.

위상정렬은

노드 간의 순서를 결정.
항상 같은 정렬 결과를 보장하진 않음.
사이클이 존재하면 노드 간의 순서를 명확하게 정의할 수 없으므로 사이클이 없음.
O(V + E)의 시간복잡도를 가짐.(V : 노드 수, E : 에지 수)

핵심 이론

먼저 in-degree 즉, 진입 차수의 개념을 알아야한다.

진입 차수는 자기 자신을 가리키는 에지의 개수를 나타내는 것을 의미한다.

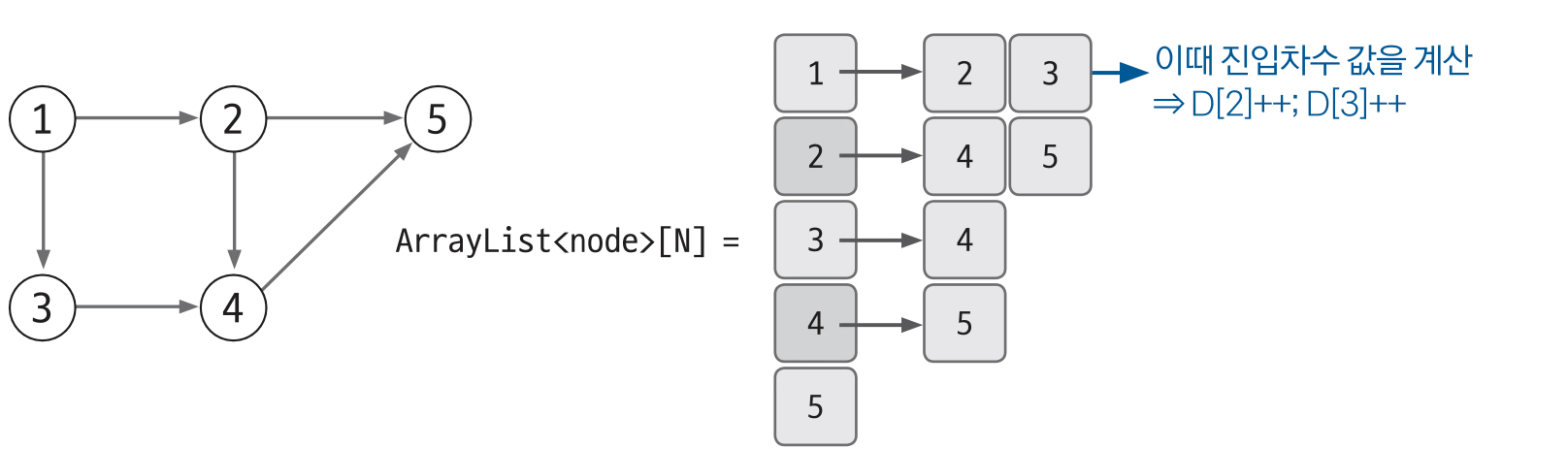
아래는 ArrayList로 사이클이 없는 그래프를 표현한 것이다.

위상 정렬 1 Do it! 알고리즘 코딩 테스트

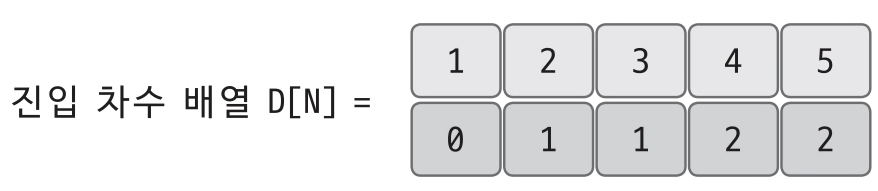
위의 그래프에서 본인을 가르키는 노드의 개수를 진입 차수 배열로 나타낸다.

1에서 2와 3을 가리키기에 D[2], D[3]을 각각 1씩 증가시킨다.

위상 정렬 2 Do it! 알고리즘 코딩 테스트

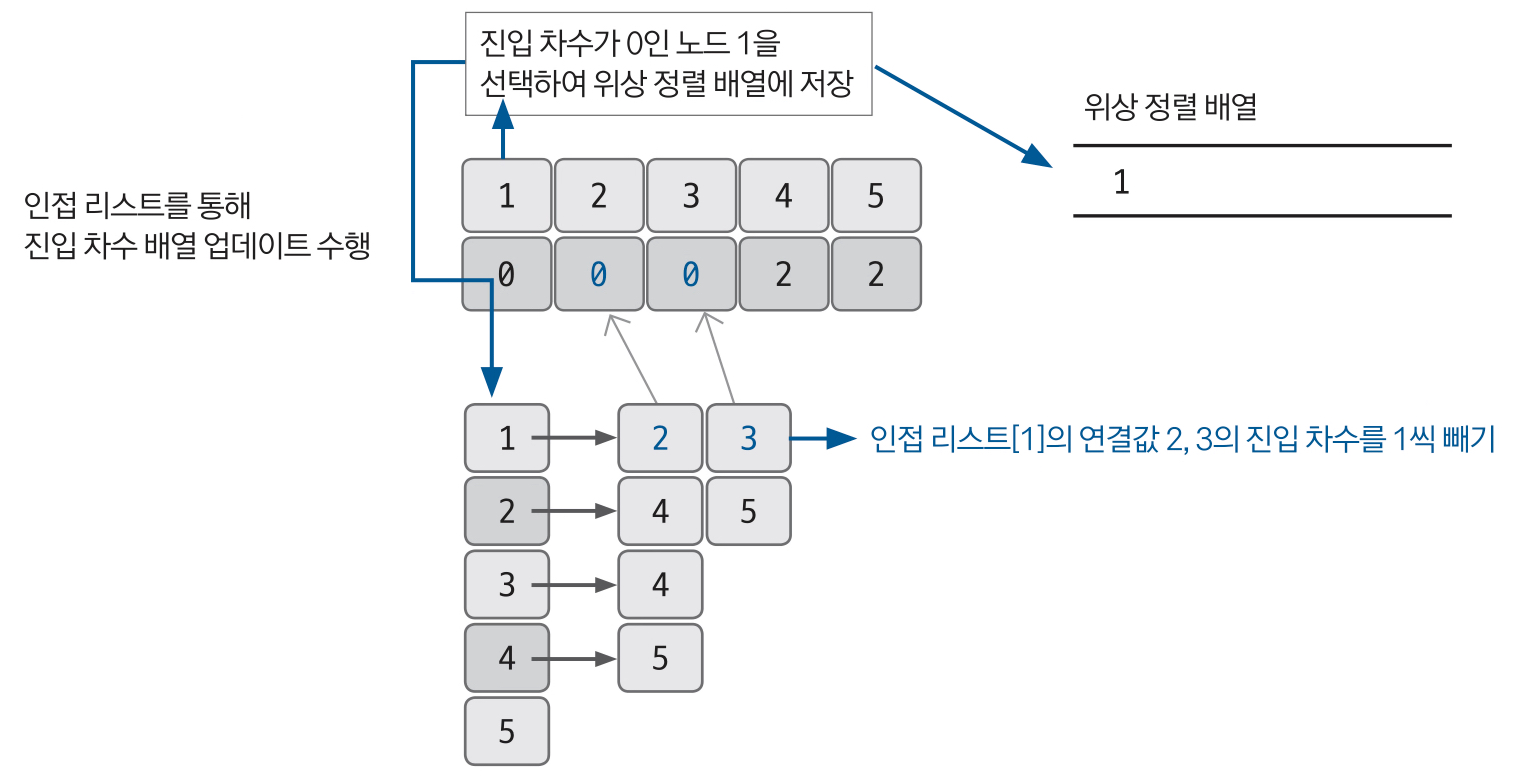
이후 진입 차수 배열에서 진입 차수가 0인 노드를 선택하여 선택된 노드를 정렬 배열에 저장한다.

이후 인접 리스트에서 선택된 노드라 가리키는 노드들의 진입 차수를 1씩 뺀다.

위상 정렬 3 Do it! 알고리즘 코딩 테스트

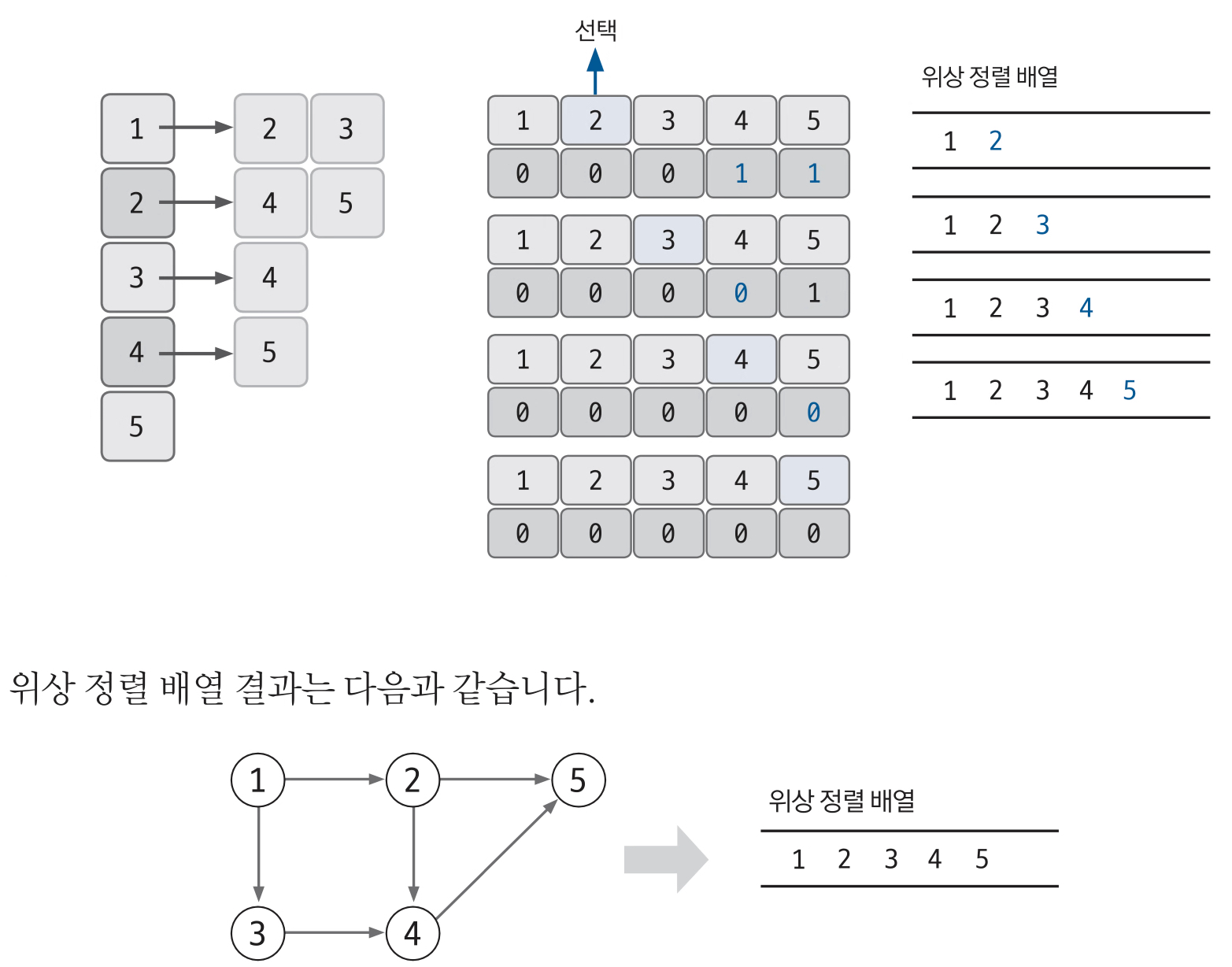
2와 3이 0이 되었기에 2번과 3번 중 하나를 선택하여 위상 정렬 배열에 넣어준다.

2와 3을 모두 선택할 수 있으니 2를 먼저 선택했을 때와 3을 먼저 선택했을 때의 결과가 다르기에 위에서 설명한 “항상 같은 정렬 결과를 보장하진 않음.”의 내용이 성립된다.

위상 정렬 4 Do it! 알고리즘 코딩 테스트

위의 예시에서는 2를 먼저 선택하는 루트로 설명하였다.

문제를 풀기 전에 알고 가면 좋은 것들을 보고 가자.

문제에서 출력의 내용을 보면 “답이 여러 가지인 경우에는 아무거나 출력한다.” 라는 내용은 위상 정렬의 “항상 같은 정렬 결과를 보장하진 않음.” 이라는 내용와 상통되니 해당 내용으로 위상 정렬 문제라는 것의 힌트를 얻을 수 있다.

구현 시 위상 정렬의 수행 과정은

진입 차수가 0인 노드를 큐에 저장(offer).
큐에서 데이터를 poll하여 해당 노드를 탐색 결과에 추가, 해당 노드가 가리키는 노드의 진입 차수를 1씩 감소한다.
감소했을 때 진입 차수가 0이 되는 노드를 큐에 저장(offer)한다.
큐가 빌 때까지 위의 과정을 반복한다.

아래의 문제를 풀어보며 위상 정렬을 익혀보자.

https://www.acmicpc.net/problem/2252

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        // 학생 수
        int N = sc.nextInt();

        // 비교 회수, 진입 차수를 초기화하는데 사용한다.
        int M = sc.nextInt();

        // 데이터 저장 인접 리스트
        ArrayList<ArrayList<Integer>> A = new ArrayList<>();

        for (int i = 0; i <= N; i++){
            A.add(new ArrayList<>());
        }

        // 진입 차수 배열
        int[] indegree = new int[N +1];

        // 그래프 초기화
        for(int i = 0; i < M; i++){
            int S = sc.nextInt();
            int E = sc.nextInt();

            A.get(S).add(E);

            // S가 E를 가르니 E의 진입 차수를 더한다.
            indegree[E]++;
        }

        // 위상 정렬 수행
        Queue<Integer> queue = new LinkedList<>();

        for (int i = 1; i<= N; i++){
            // 진입 차수가 0인 노드를 큐에 넣는다.
            if(indegree[i] == 0){
                queue.offer(i);
            }
        }

        while(!queue.isEmpty()){
            // 진입 차수가 0이었던 노드 값을 읽어온다.
            int now= queue.poll();

            // 진입 차수로 정렬된 위상 정렬을 순서대로 출력한다.
            System.out.print(now + " ");

            // 초기화한 그래프를 토대로 현재 노드에서 갈 수 있는 노드를 탐색
            for (int next : A.get(now)){
                // 방문한 노드의 진입 차수를 감소한다.
                indegree[next]--;

                // 감소 시킨 진입 차수가 0이라면 큐에 넣는다.
                if(indegree[next] == 0){
                    queue.offer(next);
                }
            }
        }
    }
}

Ref.

Do it! 알고리즘 코딩 테스트 - 자바 편, 이지스퍼블리싱/김종관 저

재훈맨

[Coding Test] 그래프 -1-

그래프의 표현

Edge List, 에지 리스트

에지 리스트로 그래프 표현하기.

Adjacency matrix, 인접 행렬

인접 행렬로 그래프 표현하기

Adjacency list, 인접 리스트

인접 리스트로 그래프 표현하기

Union-find, 유니온 파인드

핵심 이론

Union 연산

Find 연산

1. 처음에는 노드가 서로 연결되지 있지 않으므로 각 노드가 대표 노드가된다.

2. 2개의 노드를 선택하여 각각의 대표 노드를 찾아 연결하는 union 연산을 수행한다.

3. 자신이 속한 집합의 대표노드를 찾는 find 연산을 수행한다.

4. find 연산을 수행하여 시간 복잡도를 최적화한다.

Topology Sort, 위상 정렬

핵심 이론

참고

[Architecture] 소프트웨어 아키텍처 패턴

[Database] 데이터의 기본 탐색 기법과 구조

[Database] Database Index - 적용 part 2.

[Database] Database Index - 적용 part 1.