[Coding Test] 정수론
정수론은 수학에서 수의 성질을 탐구하고 공부하는 분야이다.
코딩 테스트에서는 정수론을 깊게 탐구하는 것은 아니기에 가장 많이 활용하는 몇 가지 정수론을 학습할 것이다.
소수
Prime number, 소수는 자신보다 작은 2개의 자연수를 곱해 만들 수 없는 1보다 큰 자연수를 의미한다.
좀 더 쉬운 의미로는 1과 자기 자신 외에 약수가 존재 하지 않는 수를 의미한다.
핵심 이론
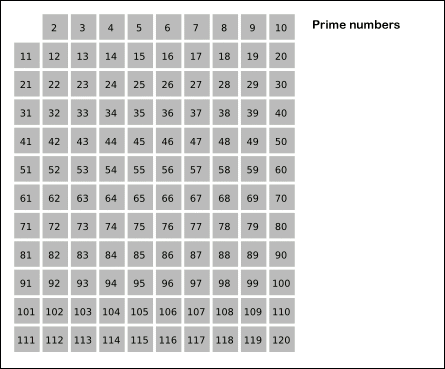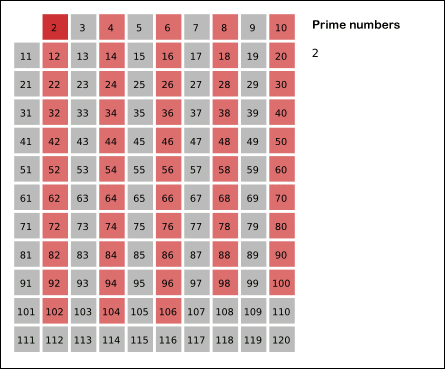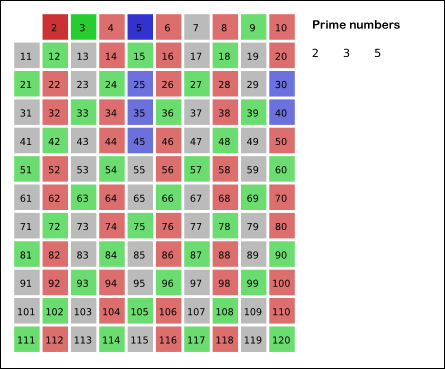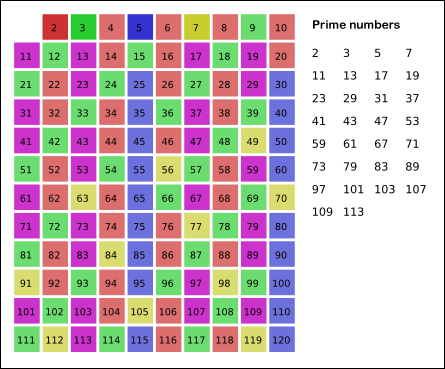
소수를 구할 때는 대표적으로 에라토스테네스의 체를 활용한다. 이는,
- 구하고자하는 소수의 범위 만큼 1차원 배열을 생성한다.
- 시작은 2부터 시작하여 지워 지지 않은 수들을 선택하고, 해당 수의 배수에 해당하는 수를 배열에서 끝까지 탐색하며 지운다.
- 배열에 끝까지 2번의 과정을 반복하여 배열에 남아있는 모든 수를 출력한다.
https://ko.wikipedia.org/wiki/%EC%97%90%EB%9D%BC%ED%86%A0%EC%8A%A4%ED%85%8C%EB%84%A4%EC%8A%A4%EC%9D%98_%EC%B2%B4
에라토스테네체의 시간 복잡도는 O(Nlog(logN))이다.
아래의 문제를 풀며 에라토스테네체를 이용한 소수 구하기를 익혀보자.
https://www.acmicpc.net/problem/1929
참고로 N의 제곱근 까지만 탐색하는 이유는 N이 a*b라 가정 했을 때 a,b는 모두 N의 제곱근보다 클 수 없다.
16의 범위까지 소수를 구할 때도 16 = 4*4로 이뤄지면 작은 숫자는 항상 4보다 작은 약수를 갖게된다.
그렇기에 16일 때는 4까지만 소수를 판별하면된다.
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int M = sc.nextInt();
int N = sc.nextInt();
int[] A = new int[N + 1];
// 초기화
// 2부터 값을 넣는다.
for(int i = 2; i<=N; i++){
A[i] = i;
}
// 탐색은 제곱근 까지만
for(int i = 2; i <= Math.sqrt(N); i++){
// 이미 지워진 값이라면 다음 루프로 넘어간다.
if(A[i] == 0){
continue;
}
// 0으로 설정하여 배수 지우기
for(int j = i + i; j <= N; j = j + i){
A[j] = 0;
}
}
for(int i = M; i <= N; i++){
if(A[i] != 0){
System.out.println(A[i]);
}
}
}
}
오일러 피
오일러 피 함수 P[N]의 정의는 1~N의 범위에서 N과 서로소인 자연수의 개수를 의미한다.
여기서 서로소는 GCD(최대공약수) 1인 두 자연수를 의미한다.
핵심 이론
원리는 에라토스테네스의 체와 비슷하다.
- 구하고자 하는 오일러 피의 범위 만큼 배열을 초기화.
- 2부터 시작하여 N의 제곱근까지 탐색하며 소인수 일 때 현재 숫자(K)의 배수에 해당하는 수를 배열 끌까지 탐색하며
P[i] = P[i] - P[i]/k연산을 수행한다. - 배열 끝까지 2번을 반복하여 오일러 피 함수를 완성한다.
아래의 문제를 풀고 오일러 피를 이해해보자.
문제를 풀기전에 위에서 언급 하였듯이 GCD가 1이라는 것은 오일러 피를 의미하며 문제에 나와있는 GCD(n,k) = 1의 의미도 오일러 피를 구하라는 의미로 해석할 수 있다.
https://www.acmicpc.net/problem/11689
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
long n = Long.parseLong(br.readLine());
long result = n;
// 제곱근까지 탐색.
for(long p = 2; p <= Math.sqrt(n); p++){
// 현재 선택된 수가 나눴을 때 0이 나온다면.
// 즉 소인수에 해당된다면.
if( n % p == 0 ){
//결과값 연산
result = result - result / p;
// 연산이 완료된 소인수는 다음연산을 위해 나누기 연산으로 삭제한다.
// 45를 기준으로 45 = 3^2 * 5 이며
// 소인수에 해당하는 3을 삭제하기 위해
// ((3*(3/3))/3) * 5 를 수행하여 5만 남긴다.
while ( n % p == 0){
n /= p;
}
}
}
// 제곱근 까지만 탐색하며 1개인 소인수가 누락될 수 있기에
// 남아있을 수 있는 소인수 구성을 지운다.
if( n > 1 ){
result = result - result / n;
}
System.out.println(result);
}
}
유클리드 호제법
두 수의 최대공약수(GCD, Greatest Common Divisor)를 구하는 알고리즘이다.
일반적으로 GCD를 구할 때는 소인수분해를 이용해 공통된 소수들의 곱으로 표현할 수 있지만 유클리드 호제법은 이를 더 간단한 방법으로 구할 수 있다.
핵심 이론
나머지 연산(MOD, %)을 이용하여 GCD를 판별할 수 있다.
- 큰 수를 작은 수로 나눠 나머지를 구한다.
- 앞의 연산에서 사용한 작은 수를 구한 나머지로 다시 나머지 값을 계산한다.
- 나머지가 0이 되었을 때의 작은수를 GCD로 선별한다.
270과 192를 기준으로 계산하자면
gcd(270, 192)
270 % 192 = 78
192 % 78 = 36
78 % 36 = 6
36 % 6 = 0
gcd(270, 192) = 6
와 같이 6의 GCD를 도출해낼 수 있다.
또한 GCD를 안다면 최소공배수(LCM,Least Common Multiple) 를 구하는데 사용할 수 있다.
LCM(a,b) = a * b / GCD(a, b).
아래의 문제를 풀면서 유클리드 호제법을 이용한 GCD, LCM 을 이해해보자.
https://www.acmicpc.net/problem/1934
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int t = sc.nextInt();
for(int i = 0; i < t; i++){
int a = sc.nextInt();
int b = sc.nextInt();
int result = a * b / gcd(a, b);
System.out.println(result);
}
}
static int gcd(int a, int b){
if( b == 0 ){
return a;
}
// 재귀 방식으로 호출하여 나머지가 0이 되었을 때의 a를 구한다
else {
return gcd(b, a % b);
}
}
}
확장 유클리드 호제법
기존 유클리드 호제법에서는 두 수의 GCD를 구하는 것만 표현했다면 이를 확장하여 방정식의 해를 구할 것이다.
핵심 이론
해를 구하는 방정식은 아래와 같다.
ax + by = c
위의 방적식은 c % gcd(a, b) = 0 인경우에만 정수해를 가진다.
즉, c가 a와 b의 최대 공약수의 배수인 경우에만 정수해를 가진다는 것이다.
다시 풀어서 얘기하자면 ax + by = c에서 c의 최솟값이 GCD(a, b)라는 것을 의미한다.
위의 이론으로 인해 ax + by = gcd(a, b)의 베주 항등식이 성립되며 확장 유클리드 호제법은 해당 식에 맞는 x, y를 구하는 알고리즘이다.
여기서 베주 항등식은 두 수의 GCD를 두 수의 배수의 합으로 나타낼 수 있는 식이다.
구현을 위해서는
- 기본 유클리드 호제법을 사용하여 GCD를 구함.
- 각 단계에서 역추적하여 계수 x와 y를 구한다.
- 반복을 통해
ax + by = gcd(a, b)에 만족하는 x와 y를 구한다.
5x + 9y = 2일 때를 예시로 들어보겠다.
먼저 5와 9의 GCD는 1이며, 2는 GCD인 1의 배수이기 때문에 확장 유클리드 호제법을 적용할 수 있다.
2를 GCD의 값으로 바꾸는 과정을 수행하겠다.
ax + by = gcd(a, b)에 의해 5x + 9y의 GCD는 1이 되고, 식을 다시 5x + 9y = 1로 두고 시작한다.
a,b로 유클리드 호제법을 나머지가 0이 될 때까지 반복하여 몫과 나머지를 저장한다.
| 식 | 나머지 | 몫 |
|---|---|---|
| 5 % 9 | 5 | 0 |
| 9 % 5 | 4 | 1 |
| 5 % 4 | 1 | 1 |
| 4 % 1 | 0 | 4 |
반복으로 구한 나머지와 몫을 역행하여 x = 이전 y y = 이전 x - 이전 y * 몫(q)
을 계산한다.
초기에는 이전 값이 없으니 x, y는 각각 1,0으로 설정한다.
즉, 가장 초기 x는 이전의 y가 되니 0, y는 이전 x(1) - 이전 y(0) * 4로 계산된다.
| 나머지 | 몫 | x | y |
|---|---|---|---|
| 0 | 4 | 0 | 1 - 0 * 4 = 1 |
| 1 | 1 | 1 | 0 - 1 * 1 = -1 |
| 4 | 1 | -1 | 1 - (-1 * 1) = 2 |
| 5 | 0 | 2 | -1 -(2 * 0) = -1 |
마지막으로 구해진 x = 2 와 y = -1을 5x + 9y = 1의 식에 대입하면
5(2) + 9(-1) = 1 가 성립된다.
아래의 문제를 풀어보며 확장 유클리드 호제법을 익혀보자.
https://www.acmicpc.net/problem/21568
import java.io.*;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int c = Integer.parseInt(st.nextToken());
long gcd = gcd(a,b);
// GCD의 배수가 아니라면 종료한다.
if( c % gcd != 0){
System.out.println(-1);
}else {
int q = (int) (c / gcd);
long[] ret = Excute(a, b);
System.out.println(ret[0] * q + " " + ret[1] * q);
}
}
static long[] Excute(long a, long b){
long[] ret = new long[2];
// 유클리드 호제법에 해당하며 가장 먼저 리턴 될 1,0 을 초기 값으로 둔다.
if( b==0 ){
ret[0] = 1;
ret[1] = 0;
return ret;
}
long q = a / b;
// 재귀 형태로 유클리드 호제법 수행
long[] v = Excute(b, a % b);
// x의 값은 이전 y 값
ret[0] = v[1];
// y의 값은 이전 x 값 - 이전 y 값 * 몫
ret[1] = v[0] - v[1] * q;
return ret;
}
// 초기 검증용 GCD
static long gcd(long a, long b){
if(b == 0){
return a;
}else {
return gcd(b, a % b);
}
}
}
Ref.
Do it! 알고리즘 코딩 테스트 - 자바 편, 이지스퍼블리싱/김종관 저