[Coding Test] 탐색 기법

2024년 6월 19일 8 분 소요

데이터 구조에서 특정 데이터를 찾기 위한 알고리즘이다.

일반적으로 데이터베이스, 파일 시스템, 네트워크, 메모리 내 데이터 구조 등에서 특정 데이터를 찾는 데 사용되며, 탐색 알고리즘은 데이터 구조와 탐색할 데이터의 종류에 따라 다양한 방식이 있다.

DFS, Depth First Search, 깊이 우선 탐색

그래프 완전 탐색 기법 중 하나이다.

그래프의 시작 노드에서 출발하여 탐색할 한 쪽 분기를 최대 깊이까지 탐색을 마친 후 다른 쪽 분디로 이동하여 다시 탐색을 수행하는 알고리즘이다.

일종의 Backtracking 알고리즘이라 할 수 있다.

특징

재귀 함수로 구현
Stack 자료구조 이용

시간 복잡도

O(V + E)

V: 노드 수, E: 에지 수

실제 구현하는데 재귀 함수를 사용하기에 Stack Overflow에 유의해야한다.

단절점/선 찾기, 사이클 찾기, 위상 정렬 등에 사용한다.

핵심 이론

한 번 방문한 노드를 다시 방문하지 않기에 노드 방문 여부를 체크할 배열이 필요하다.

ArrayList 등을 사용하여 인접 요소들을 그래프를 표현한다.

DFS의 탐색 방식은 후입선출 특성을 가지기에 Stack을 사용할 수 있지만 보통은 재귀 함수로 많이 구현한다.

과정

DFS를 시작할 노드를 정한 뒤 방문 했다는 표시를 한다.
해당 노드의 인접 노드를 방문한다.
인접 노드가 없을 떄 까지 즉, 최대 깊이까지 반복한다.
부모 노드로 올라가면서 방문하지 않은 노드가 있다면 이를 탐색한다.
방문하지 않은 노느도 위와 같은 과정을 반복한다.
모든 노드를 탐색한다면 종료한다.

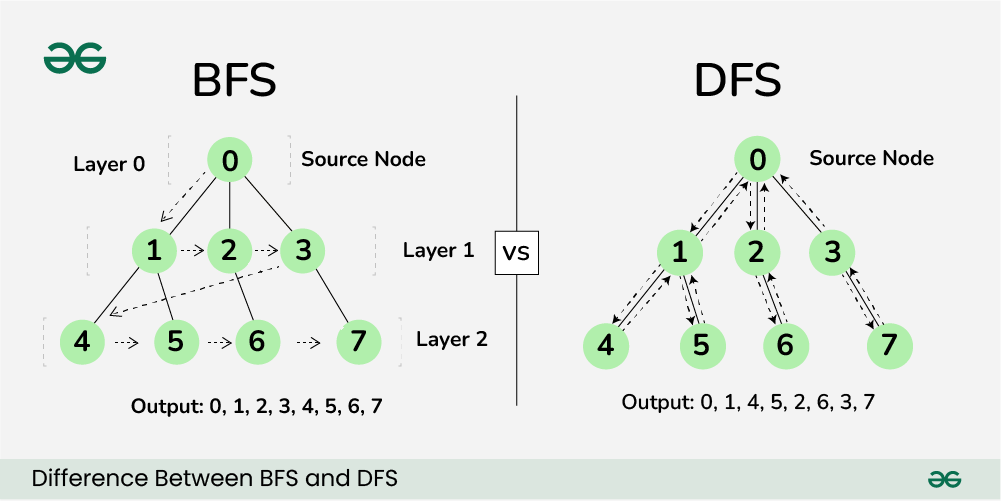DFS/BFS https://www.geeksforgeeks.org/difference-between-bfs-and-dfs/

아래의 문제로 DFS를 익혀보자.

https://www.acmicpc.net/problem/11724

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.StringTokenizer;

public class Main {

    // 인접 리스트 선언.
    static ArrayList<Integer>[] A;
    // 방문한 노드 표시 배열 선언.
    static boolean[] visited;

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        // 정점의 개수
        int N = Integer.parseInt(st.nextToken());

        // 간선의 개수
        int m = Integer.parseInt(st.nextToken());

        A = new ArrayList[N + 1];
        visited = new boolean[N + 1];

        // 인접 리스트 초기화
        for(int i = 1; i < N+1; i++){
            A[i] = new ArrayList<Integer>();
        }

        for(int i = 0 ; i < m; i++){
            st = new StringTokenizer(br.readLine());

            int s = Integer.parseInt(st.nextToken());
            int e = Integer.parseInt(st.nextToken());

            // 방향 없는 그래프이기에 양쪽 모두 에지를 더하기.
            A[s].add(e);
            A[e].add(s);
        }

        int count = 0;

        for(int i = 1; i < N + 1; i++ ){
            //방문하지 않은 노드가 없을 때 까지.
            if(!visited[i]){
                //DFS가 2번 이상 수행 됐다는 것은 그룹이 나눠졌다는 의미.
                count++;
                DFS(i);
            }
        }

        System.out.println(count);
    }

    static void DFS(int v){

        // 현재 노드를 이미 방문했다면 더 할 필요가 없다.
        if(visited[v]){
            return;
        }

        //노드 방문 표시
        visited[v] = true;

        //양방향 에지에 저장한 요소들을 순회하면서
        for(int i : A[v]){
            //노드 안에 있는 에지 중 방문하지 않은 요소가 있다면
            if (!visited[i]){
                //재귀
                DFS(i);
            }
        }
    }

}

BFS, Breadth First Search, 너비 우선 탐색

너비 우선 탐색 또한 그래프를 완점 탐색하는 방법 중 하나다.

시작 노드에서 출발하여 이를 기준으로 가까운 노드를 먼저 방문하는 탐색 알고리즘이다.

특징

FIFO 탐색
Queue 자료구조 이용

시간 복잡도

O(V + E)

V: 노드 수, E: 에지 수

핵심 이론

BFS 또한 DFS처럼 방문한 노드는 다시 방문하지 않기 때문에 방문 노드를 체크하기 위한 배열이 필요하다.

BFS 또한 ArrayList로 인접 요소를 그래프로 나타낼 수 있다.

탐색을 위해 스택이 아닌 큐를 사용한다.

과정

DFS를 시작할 노드를 정한 뒤 방문 했다는 표시를 한다.
해당 노드의 값을 큐에 순서대로 add한다.
가장 먼저 들어간 값의 노드를 poll 한다.
poll한 노드의 값들을 큐에 add한다.
이 때 방문한 요소는 큐에 add하지 않는다.
큐에 노드가 없을 때 까지 앞선 과정을 반복한다.

위에서 사용한 사진을 다시 참고해보자.

DFS/BFS https://www.geeksforgeeks.org/difference-between-bfs-and-dfs/

아래의 문제로 BFS를 익혀보자.

https://www.acmicpc.net/problem/1260

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {

    static boolean[] visited;
    static ArrayList<Integer>[] A;

    public static void main(String[] args) throws IOException {

        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());

        int start = Integer.parseInt(st.nextToken());

        A = new ArrayList[N+1];

        for (int i = 1; i<=N; i++){
            A[i] = new ArrayList<Integer>();
        }

        for (int i = 0; i < M; i++){
            st = new StringTokenizer(br.readLine());

            int S = Integer.parseInt(st.nextToken());
            int E = Integer.parseInt(st.nextToken());

            A[S].add(E);
            A[E].add(S);
        }

        // 방문할 수 있는 점이 여러 개인 경우
        // 낮은 번호를 먼저 방문하기 위해 정렬
        for(int i = 1; i<=N; i++){
            Collections.sort(A[i]);
        }

        // 방문점 초기화
        visited = new boolean[N+1];
        // 시작에서 부터 DFS 수행
        DFS(start);
        System.out.println();

        //다시 초기화
        visited = new boolean[N+1];
        BFS(start);
        System.out.println();
    }

    static void DFS(int node){

        System.out.print(node+" ");

        visited[node] = true;

        for(int i : A[node]){
            if(!visited[i]) {
                DFS(i);
            }
        }
    }
    
    // 너비 우선 탐색
    static void BFS(int node){
        
        //사용할 큐 선언
        Queue<Integer> queue = new LinkedList<>();

        //초기 start할 노드를 넣어준다.(while 조건문 충족)
        queue.add(node);

        // 해당 노드는 방문했다고 표시
        visited[node] = true;

        // 큐에 있는 내용이 없을 때 까지
        while (!queue.isEmpty()){
            
            // 현재 큐의 가장 앞에 있는 값을 빼오면서 현재 노드로 지정.
            int now_node = queue.poll();

            System.out.print(now_node + " ");

            //큐에서 뺀 노드가 가지고 있는 값만큼 순회
            for (int i : A[now_node]){
                //해당 요소를 방문하지 않았다면
                if(!visited[i]){
                    //방문 표시
                    visited[i] = true;
                    // 해당 요소를 큐에다 넣는다.
                    queue.add(i);
                }
            }
        }

    }
}

Binary search, 이진 탐색

데이터가 정렬돼 있는 상태에서 원하는 값을 찾아내는 알고리즘이다.

데이터의 중앙값과 찾고자 하는 값을 비교해 데이터의 크기를 절반씩 줄이면서 대상을 찾는 탐색법이다.

특징

중앙값 비교를 통한 대상 축소 방식

시간 복잡도

O(logN)

구현 및 원리가 비교적 간단하여 코딩 테스트에서 부분 문제로 많이 요구된다.

핵심 이론

데이터가 정렬되어 있어야 한다.

데이터 셋의 중앙값과 타겟 데이터의 크기를 비교하여 데이터셋의 왼쪽과 오른쪽을 선정한다.

과정

오름차순으로 정렬된 데이터에서 다음 과정을 반복한다.

현재 데이터셋의 중앙값(Median)을 선택한다.
중앙값 > 타겟 데이터 : 중앙값 기준으로 왼쪽 데이터셋을 선택한다.
중앙값 < 타겟 데이터 : 중앙값 기준으로 오른쪽 데이터셋을 선택한다.
위의 과정을 반복하다가 중앙값 == 타겟 데이터일 때 탐색을 종료한다.

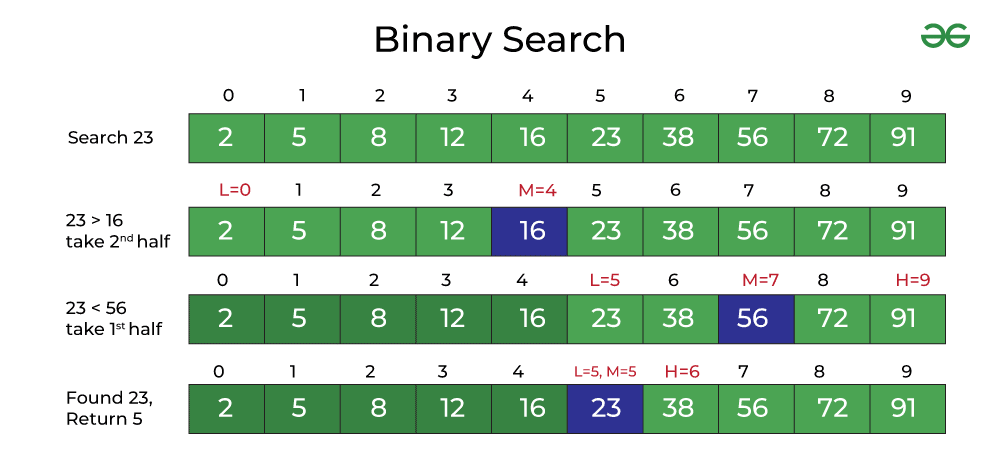https://www.geeksforgeeks.org/binary-search-in-java/

아래의 문제로 이진탐색을 익혀보자.

https://www.acmicpc.net/problem/1920

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        StringTokenizer st = new StringTokenizer(br.readLine());

        int N = Integer.parseInt(st.nextToken());

        st = new StringTokenizer(br.readLine());

        int[] A = new int[N];

        for(int i = 0; i<N; i++){
            A[i] = Integer.parseInt(st.nextToken());
        }
        // 이분 탐색을 위한 정렬
        // java의 기본 정렬은 O(nlogn)이다.
        Arrays.sort(A);

        st = new StringTokenizer(br.readLine());

        // 찾아야하는 숫자 개수
        int M = Integer.parseInt(st.nextToken());

        st = new StringTokenizer(br.readLine());

        for (int i = 0; i<M; i++){

            boolean find = false;

            // 찾으려는 타겟 값
            int target = Integer.parseInt(st.nextToken());

            //이진 탐색 시작

            //초기에는 배열 전체를 스코프로 둔다.
            int start = 0;
            int end = A.length - 1;

            // 범위가 최대로 좁혀질 때까지
            while (start <= end){
                
                //중간 인덱스와 중간 값
                int mid = (start + end) / 2;
                int mid_value = A[mid];

                // 타겟이 작으니 왼쪽
                if (mid_value > target){
                    end = mid -1;
                }
                // 타겟이 크니 오른쪽
                else if (mid_value < target) {
                    start = mid + 1;
                }
                // 타겟과 중앙값이 같다.
                else {
                    find = true;
                    break;
                }
            }

            if(find){
                System.out.println(1);
            } else{
                System.out.println(0);
            }
        }
    }
}

Ref.

Do it! 알고리즘 코딩 테스트 - 자바 편, 이지스퍼블리싱/김종관 저

재훈맨

[Coding Test] 탐색 기법

DFS, Depth First Search, 깊이 우선 탐색

특징

시간 복잡도

핵심 이론

과정

BFS, Breadth First Search, 너비 우선 탐색

특징

시간 복잡도

핵심 이론

과정

Binary search, 이진 탐색

특징

시간 복잡도

핵심 이론

과정

참고

[Architecture] 소프트웨어 아키텍처 패턴

[Database] 데이터의 기본 탐색 기법과 구조

[Database] Database Index - 적용 part 2.

[Database] Database Index - 적용 part 1.