재훈맨

Java/Spring Boot 백엔드 개발자

2 분 소요

시간 복잡도는 문제를 해결하기 위한 연산 횟수를 의미한다.

시간 복잡도는 상황별로 유형을 나눠서 표기한다.

시간 복잡도 유형

  • Big-Omega, Ω(n) : 최선일 때 (Best)
  • Big-Theta, θ(n) : 보통일 때 (Average)
  • Big-O, O(n) : 최악일 때 (Worst)

for 문을 이용하여 0~99까지 숫자를 출력하는 프로그램이 있을 때 각 시간 복잡도는

  • Big-Omega : 1번
  • Big-Theta : N/2번
  • Big-O : N번

와 같이 표시할 수 있다.

코딩테스트에서는 최대한 많은 케이스를 성공적으로 성공해야하기에 최악의 테스트 케이스를 통과하는 것을 기준으로 잡는다.

의미인 즉슨 Big-O를 기준으로 하여 시간 복잡도를 고려해야한다.

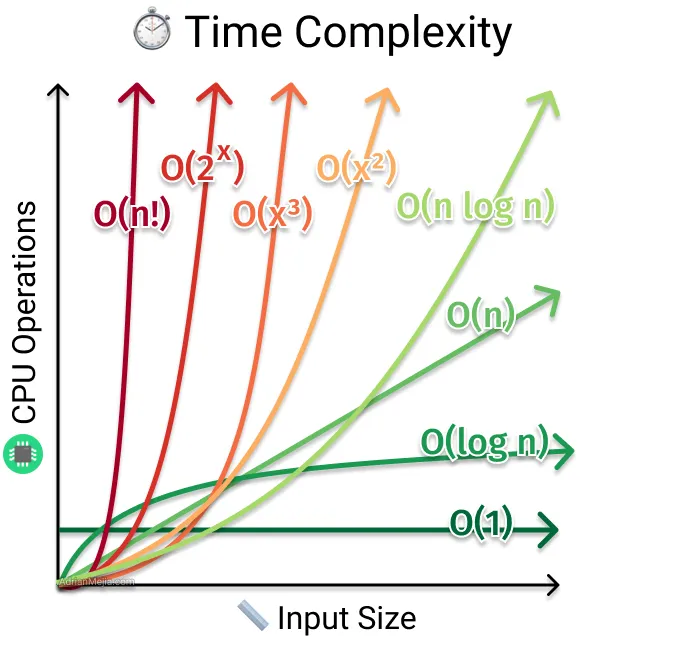시간복잡도 표 https://praveendavidmathew.medium.com/big-o-notation-understanding-different-time-complexities-72fe847a6343

위의 Big-O의 시간 복잡도 그래프를 보게된다면 데이터의 크기에 따라 성능이 달라지는 것을 알 수 있다.

시간 복잡도 활용하기

코딩 테스트 문제를 풀 때 “시간 제한” 이라는 항목이 존재할 수 있다.

보통은 초 단위를 많이 보게될텐데 1초당 1억번의 연산을 하는 것으로 기준을 잡는다.

이는 1초당 1억번의 연산을 하는 것을 최악의 경우라고 판단하기 때문이다.

연산 횟수 계산하기

여기서 연산 횟수를 계산하는 식을 활용할 수 있는데

연산 횟수 = 시간 복잡도 * 데이터 크기

와 같다.

버블 정렬과 병합 정렬의 시간 복잡도는 각각 O(n^2), O(n log n)인데 이를 토대로 시간 제한이 2초(200,000,000)인 코딩 테스트의 연산 횟수를 계산 해보자면

버블 정렬 = (1,000,000)^2 = 1,000,000,000,000 

병합 정렬 = 1,000,000 log (1,000,000) = 약 20,000,000

와 같은 계산 결과가 나오고 버블 정렬은 2초를 넘고, 병합 정렬은 2초 미만의 연산 횟수를 진행하기에 병합 정렬을 이용하면 적적하게 문제를 풀 수 있음을 가늠할 수 있다.

이처럼 연산 횟수로 적절한 알고리즘을 활용할 수 있음을 알 수 있다.

시간 복잡도 도출

코드의 시간 복잡도를 도출하여 이를 개선하기 위해선 일단 코드에서 시간 복잡도를 도출해야한다.

시간 복잡도 도출 기준은

  • 상수 제외.
  • 가장 많이 중첩된 반복문 기준.

와 같다.

위의 기준이라면 for문을 1번 이용하여 연산 횟수가 N인 코드와 for문 3번 사용하여 3N의 연산 횟수를 가진 코드들은 모두 O(n)이 된다.

또한 2중 for문이 사용된 코드는 이것이 기준이 되어 O(n^2)이된다.

코딩 테스트에 응시할 때 시간, 메모리 제한이 있을 때 시간 복잡도를 계산하고 어떤 알고리즘을 써야하는지, 정렬을 수행할 수 있는지 등을 판단할 수 있는 기반이 되는 지식이다.


Ref.

Do it! 알고리즘 코딩 테스트 - 자바 편, 이지스퍼블리싱/김종관 저

참고